Mishmash
HW used:
This project comes in as unmixed mishmash. It has kind of self of naive Diffie–Hellman key exchange implementation. For DHKE it uses Earth magnetic field measurements. Touches safe primes thefore Sophie Germain primes and some mathematical function optimizations and stack-only implementations. This all only to use DHKE key as input to color picking for lighting RGB LED up.
Points of interest
If you are interested in some of topics mentioned, simply use your favorite search engine on respective term or check some of bellow.
- Sophie Germain Prime on Wolfram Mathworld
- Safe and Sophie Germain primes explained
- Strong prime
- A005385 Safe primes p: (p-1)/2 is also prime
- A005384 Sophie Germain primes p: 2p+1 is also prime
- A051634 Strong primes: prime(k) > (prime(k-1) + prime(k+1))/2
Okay then. Let jump onto first batch of code.
The Hearth of the House 🌐
Whence all other is called, entry function. Let check with its contents 1st and move after to interesting details of employed surroundings.
#![no_main]
#![no_std]
use cortex_m::prelude::_embedded_hal_blocking_delay_DelayMs;
use cortex_m_rt::entry;
use lsm303agr::{Lsm303agr, MagMode, MagOutputDataRate};
use microbit::hal::pac::twim0::frequency::FREQUENCY_A;
use microbit::hal::time::U32Ext;
use microbit::hal::{Delay, Rng, Twim};
use microbit::pac::PWM0;
use microbit::Board;
use panic_halt as _;
use crate::CheckCondition::{GeneratorGreaterOrEqualToPrime, GeneratorLessThenTwo, Ok};
use microbit::hal::gpio::Level;
use microbit::hal::pwm::{
Channel::{self, C0 as CHRED, C1 as CHGREEN, C2 as CHBLUE},
CounterMode, Prescaler, Pwm,
};
const SAF_PRI_COU: usize = 49;
static SAF_PRIMES: [u16; SAF_PRI_COU] = [
5, 7, 11, 23, 47, 59, 83, 107, 167, 179, 227, 263, 347, 359, 383, 467, 479, 503, 563, 587, 719,
839, 863, 887, 983, 1019, 1187, 1283, 1307, 1319, 1367, 1439, 1487, 1523, 1619, 1823, 1907,
2027, 2039, 2063, 2099, 2207, 2447, 2459, 2579, 2819, 2879, 2903, 2963,
];
const MAX_DUTY: u16 = 512 as u16;
const MAX_AMOUNT: u16 = 1;
const HALF_AMOUNT: u16 = MAX_DUTY / 2;
#[entry]
fn entry() -> ! {
let b = Board::take().unwrap();
let mut rng = Rng::new(b.RNG);
let mut del = Delay::new(b.SYST);
let i2c = Twim::new(b.TWIM0, b.i2c_internal.into(), FREQUENCY_A::K100);
let mut e_compass = Lsm303agr::new_with_i2c(i2c);
e_compass.init().unwrap();
e_compass
.set_mag_mode_and_odr(&mut del, MagMode::LowPower, MagOutputDataRate::Hz10)
.unwrap();
let mag_con = e_compass.into_mag_continuous();
let mut mag_con = match mag_con {
core::result::Result::Ok(mc) => mc,
_ => panic!(),
};
let pwm0 = Pwm::new(b.PWM0);
pwm0.set_counter_mode(CounterMode::Up)
.set_prescaler(Prescaler::Div4)
.set_period(7810.hz());
let pins = b.pins;
pwm0.set_output_pin(
CHRED,
pins.p0_02.into_push_pull_output(Level::Low).degrade(),
)
.set_output_pin(
CHGREEN,
pins.p0_03.into_push_pull_output(Level::Low).degrade(),
)
.set_output_pin(
CHBLUE,
pins.p0_04.into_push_pull_output(Level::Low).degrade(),
);
let mut prime_ix = 0;
loop {
set_duty(&pwm0, CHRED, MAX_AMOUNT);
set_duty(&pwm0, CHBLUE, MAX_AMOUNT);
set_duty(&pwm0, CHGREEN, MAX_AMOUNT);
del.delay_ms(250u32);
let mag_sta = mag_con.mag_status();
if mag_sta.is_err() {
continue;
}
let mag_sta = unsafe { mag_sta.unwrap_unchecked() };
if !mag_sta.xyz_new_data() {
continue;
}
let mag_fie = mag_con.magnetic_field();
if mag_fie.is_err() {
continue;
}
let mag_fie = unsafe { mag_fie.unwrap_unchecked() };
let uns = mag_fie.xyz_unscaled();
fn sq(num: i16) -> i32 {
(num as i32).pow(2)
}
let x_sq = sq(uns.0);
let y_sq = sq(uns.1);
let z_sq = sq(uns.2);
let vec_mag = herons_sqrt((x_sq + y_sq + z_sq) as u16);
let sp = SAF_PRIMES[prime_ix];
prime_ix = ((prime_ix as i32 + 1) % SAF_PRI_COU as i32) as usize;
let vec_mag = vec_mag as u16;
let ck = cond_ck(vec_mag, sp);
let (d_amount, r_amount, g_amount, b_amount) = if ck == CheckCondition::Ok {
let sp = to_decimals(sp);
let sp = sp.as_slice();
let gen = to_decimals(vec_mag);
let gen = gen.as_slice();
let (alice_sec, alice_rem) = private_generation(&mut rng, &gen, &sp);
let (bob_sec, bob_rem) = private_generation(&mut rng, &gen, &sp);
let akey = shared_generation(bob_rem, alice_sec, &sp);
let bkey = shared_generation(alice_rem, bob_sec, &sp);
assert_eq!(akey, bkey);
let flags = key_typ(akey);
match flags {
// 0 < gen < prime ⇒ rem > 0
// gen ÷ prime = a ∧ ⌊a⌋ = a ⇒ rem = 0
//
// (if floor signs above are inverted, it is bug in browser,
// try copy-paste to verify)
//
0 => panic!("0 key"),
1 => (1000, 0, 0, MAX_AMOUNT), // odd, blue
2 => (1000, 0, MAX_AMOUNT, 0), // even, green
5 => (1200, HALF_AMOUNT, HALF_AMOUNT, 0), // odd prime, yellow
6 => (1500, HALF_AMOUNT, 0, HALF_AMOUNT), // even prime, purple
13 => (2500, 0, HALF_AMOUNT, HALF_AMOUNT), // safe prime, always odd, cyan
_ => panic!("unsupported flag"),
}
} else {
(150u32, MAX_AMOUNT, 0, 0)
};
set_duty(&pwm0, CHRED, r_amount);
set_duty(&pwm0, CHBLUE, b_amount);
set_duty(&pwm0, CHGREEN, g_amount);
del.delay_ms(d_amount);
}
}First Things First
1st strike: already mentioned A005385, safe prime numbers — used in DHKE computations. 2nd: some constants for PWM regulation bellow discussed in more fine detail.
Initiations are clear by themselves. Random number generator used in DHKE is created. See also Struct microbit::hal::Rng. Delay is created that is used simply for extending period of LED color uptime. Similarly magnetometer is used for generator in DHKE.
What is not so obvious is PWM set up. Prescaler Prescaler::Div4 divides base frequency by 4 where base is 16 MHz. Period of 7 810 MHz further divides frequency resulting in ≈ 512 Hz. This represents available amount of points for R,G,B channels. CounterMode::Up does service of ending all channels uptime at same time. Inspect documentation on CounterMode::UpAndDown, if applicable.
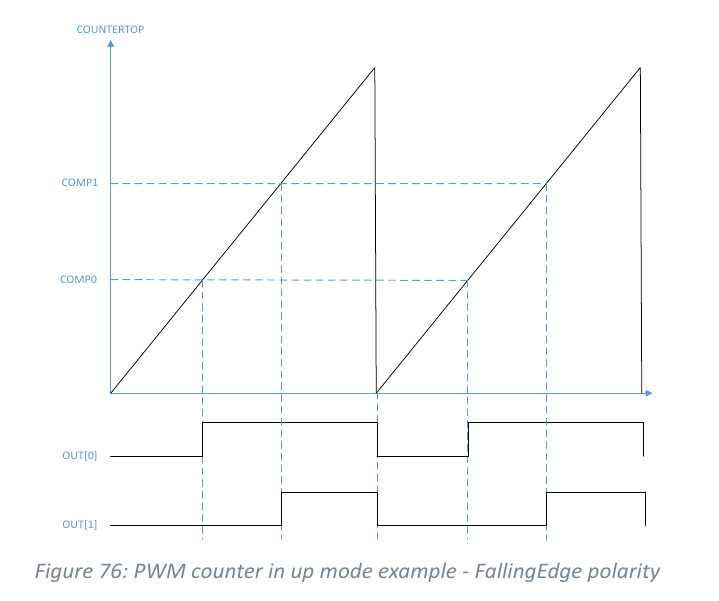
Twirling the Loop
Max and min (0) duty effectively mean no pulse. At each loop start amount on each channel is set to MAX_AMOUNT which results in white light indicating ongoing computation.
Next magnetic field measurement is obtained. Since its values are used only for DHKE generator, no calibration of sensor is needed. For remarkable reference on what generator is, check hi-quality article Diffie-Hellman Key Exchange by Eli Bendersky.
Any other source of randomness could be used. Same as only some axis value of magnetic field. But to use field magnitude is way much interesting ― square root function is needed for it. Magnitude on surface varies depending on location. It can be greater than 20 µT / 0.2 G and lower than 70 µT / 0.7 G, T = Tesla, G = Gauss. If you are curious about your location, you can check curtly with visualization at Earth’s magnetic field.
Provided interest in vector magnitude, suggestion of excavations on www.wolframalpha.com is here.

Rationale behind i16 nums conversion to i32 in fn sq lays in fact that micro:bit computes squares with i16 extra really super slow in debug build. i32 on other hand provides result in instant. CPU specification states out that 16-bit operations are supported.
The ARM® Cortex®-M4 processor with floating-point unit (FPU) has a 32-bit instruction set (Thumb®-2 technology) that implements a superset of 16- and 32-bit instructions to maximize code density and performance.
As exercise try with i16. Hop onto next paragraph.
fn sq(num: i16) -> i16 {
num.pow(2)
}Little digression. Even with uncalibrated magnetometer, unscaled values should always |val| ⪅ 1700. Value limit is important because of fixed number places array size /discussed later/. Since limit is 2962 and √(1700² ⋅3) ≈ 2944.49, there is great tolerance. My uncalibrated measurements show values similar to (x,y,z)=(-428, 30, 644), in µT (-64.2, 4.5, 96.6). This means magnitude ≈ 116.08 µT which is beyond expected range and for instance National Centers for Environmental Information magnetic field calucator expects 49.46 µT for my coordinates. Since magnitude is expected all times to not violate limit without any fallback strategy, this has shortcoming potencial.
Reason to use safe primes is not only matter of interest. Still real world cryptography is more sophisticated. For more information one can seek through, for instance, crypto.stackexchange.com for various valuable information on this. Also Eli's article has good note on this.
Hitting another requisite for DHKE, let, at last, scrutinize what, how, where, for, … of DHKE.
Entr'acte
DHKE is communication encryption key calculation which enables encrypted communication without prior key sharing. Exactly, encryption key is established at communication start rather than any time before. It labors with one-way function where one way means having fuction output there is no straightforward way to extract arguments to it even when it is well known. References in chapter footer list divers resources on DHKE. Pick up any for further information. Your keyword is "discrete" from discrete logarithm problem.
Just in case, for simple reference on how encryption key works, check Vigenere Cipher.
Participants steps
- They publicly agree on generator g and large safe prime number p.
- They also choose they private keys which are some large numbers, a, b.
- They compute their remainders X = gx mod p, e.g A = ga mod p.
- Remainders are exchanged and key is computed using formula Ky = Xy mod p, e.g. Kb = Ab mod p.
- Ka = Kb = K, both side have key without sharing it via any channel, encrypted communication commences.
Example
Expectations varification using simple values.
- g = 13, p = 2447.
- a = 12, b = 9.
- A = 1312 mod 2447 = 1126, B = 139 mod 2447 = 1542.
- Ka = 154212 mod 2447 = 1826, Kb = 11269 mod 2447 = 1826, Ka = Kb = K.
One can quickly notice that computations work with very large numbers, e.g. 154212 = 180722607724181413194741271591938625536 even when a, b, g are essentially small numbers. Real implementation safe safe prime numbers have much greater value at size at least of 512 bits but rather 2048 bits. Similar applies to secrets a, b.
Note on g: it is not arbitrary, it conforms constraint 1 < g < p. This gurantees that remainder cannot be 0. Any product of g, powers included, is not evenly divisable by p and powers of 0 would produce zeros also. Zero remainder would imply zero key which implies either zero (=no) encryption or communication data zeroing. If g was 1, then key would be exposed directly by it since key would be also 1.
Proof
Proof is defined by formula S ≡ (gm)n ≡ gmn ≡ (gn)m ≡ gnm mod p. Where ≡ stands for congruency over modulo and S for common result. This is not exactly super obvious because DHKE does use remainder after exchange not generator. This is property of modular arithmetic and can be figured out simply.
Note: Worth noticing that this proof does not labor with trivial case when remainder exchanged is equal to original power. Since in that case proof formula is obviously valid. What would happend if a,b,g would not be large enough? Let choose a=2, b=3, g=4, p=1283, A=16, B=64, Ka=(43)2 mod 1283 = Kb=(42)3 mod 1283. Nothing interesting here.
Why different A, B can replace g? Verify what is known.
- g = 2, p = 5.
- a = 5, b = 6.
- A = 25 mod 5 = 32 mod 5 = 2, B = 26 mod 5 = 64 mod 5 = 4.
- Ka = 45 mod 5 = 1024 mod 5 = 4, Kb = 26 mod 5 = 64 mod 5 = 4, K = 230 mod 5 = 1073741824 mod 5 = 4.
- Obviously Ab ≡ Ba ≡ gab mod p and 25·6 mod 5 = 326 mod 5 = 645 mod 5 = K, Ka ≡ Kb ≡ K.
Proof is verified but why it is consequently? Have look at expressions: 1) 64 mod 5 = (4 +12 ⋅5) mod 5 which is B, 2) 645 mod 5 which is K. #1 remainder is obvious but #2 is not then. Let use help, biniomial theorem. Binomial theorem applies to polynomial of form (x +y)n. There are multiple formulas and one apt is bellow.
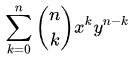
It uses binomial coefficient which can be defined as n! ÷k! ⋅(n -k)! where ! means factorial. Well known formula is for n=2, (x +y)2 = x2 +2xy +y2. Looking at binomial theorem formula, it can be worked out that last indeterminate never stands off multiplication unless in first iteration of sumation. Usually expanded expression orders accordingly to binomial as seen for y2. With same importance it can be worked out that all other terms of summation participate in multiplication with first indeterminate.
Reaching back to expression (4 +12 ⋅5) mod 5, small edit (4 +60) mod 5, binomial theorem can be applied. As deduced before, all products are evenly divisible be 60 which is, as shown, evenly divisible by 5. With exception for last one which is not since any power of 4 is not.
For clarity, summation after expansion for binomial (x +y)5 is x5 +5x4y +10x3y2 +10x2y3 +5xy4 +y5. At first glance, for x = 60 all terms are evenly divisible by 5 with exception for y5.
#2 remainder is still not obvious but it is obvious that for Ka computation is sufficient to use B, remainder, since all other terms would be evenly divisible.
Henceforth, proof is reasoned very well. It is crystal clear why formula S ≡ (gm)n ≡ gmn ≡ (gn)m ≡ gnm mod p proves also DHKE exchange computation, i.e. gab ≡ Ab ≡ Ba mod p.
Information needed to compute key are publicly sharable. Thus nothing obstructs Bob and Alice from starting key generation.
Twirling the Loop Once Again
Rest of hearth fire is quite straight. It revolves what is presented in Entr'acte sub-chapter.
- "Random", i.e. next, safe prime number is chosen.
- Magnetic field magnitude = generator is validated. When invalid, colorization is set up for red color. Colorization is meant via RGB channels and for failure indication maximal red is chosen. If valid, DHKE key computation commence.
- As already noted numbers grow really quickly. Even using very small numbers whereas this computation uses numbers of hundreds and thousands size. This is property of exponential function which is part of one-way function. Numbers cannot fit into integral data type in any means. Thus are represented as array of decimal places. More on this in specific descriptions.
- Bob and Alice compute their private results: remainder and secret. After phantasmal remainders exchange both compute keys using own secrets.
assert_eq!(akey, bkey);assures that keys are truly same. Otherwise process is aborted via panicking. - Key is then "read" as flags that are use for color selection.
- Colorization is then set up simply:
- For odd-only number maximal blue.
- For even-only number maximal green.
- For odd prime number yellow — half red, half green.
- For even prime number (2) purple — half red, half blue.
- For safe prime number cyan — half green, half blue.
- Other flags are not supported.
- Last responsibility of loop is to set up channels with chosen amounts and set up delay associated with particular color which allows colorization to be observed by human sight.
Note: As of writing this Rust Core crate misses stable version of either power for floating point data types, which could be used instead of places arrays, and square root functions.
Useful references
- pwm-demo
- pwm-blinky-demo
- Crate lsm303agr
- DT0103 Design tip
- microbit/src/09-led-compass/src/calibration.rs
- Hard & Soft Iron Correction for Magnetometer Measurements
- Binomial theorem
- Factorial
- Exponential function
- Diffie-Hellman Key Exchange:
Other amusement
Search for:
- I2C and TWI(M) compatibility
- PWM in general
- Magnetic sensor calibration on micro:bit
Variety of Auxiliaries 🌐
One type of surrounders /that stokes hearth fire with wood/ is auxiliary function and related code. There are few of them as figured by code blocks bellow.
#[derive(PartialEq)]
enum CheckCondition {
GeneratorLessThenTwo,
GeneratorGreaterOrEqualToPrime,
Ok,
}
fn cond_ck(gen: u16, sp: u16) -> CheckCondition {
return if gen < 2 {
GeneratorLessThenTwo
} else if gen < sp {
Ok
} else {
GeneratorGreaterOrEqualToPrime
};
}
fn private_generation(rng: &mut Rng, gen: &[u8], sp: &[u8]) -> (u8, u16) {
let secret = rng.random_u8();
let mut pow = pow(gen, secret);
let rem = rem(pow.as_slice_mut(), sp);
(secret, rem)
}
/// `rrem` — remote remainder, that side remainder
/// `losec` — local secret, this side secret
fn shared_generation(rrem: u16, losec: u8, sp: &[u8]) -> u16 {
let rrem = to_decimals(rrem);
let mut pow = pow(rrem.as_slice(), losec);
rem(pow.as_slice_mut(), &sp)
}1st strike — DHKE key generation related code. enum for generator validation results. Subsequent validation function with obvious responsibility. Private generation is following. It does what is expected: generates random secret in both side inclusive range 0–255, powers generator onto it and computes remainder for safe prime number. Similarly, shared generation: takes other side remainder, powers it with this side secret and computes remainder.
fn set_duty(pwm: &Pwm<PWM0>, ch: Channel, amount: u16) {
if amount == 0 {
if pwm.duty_on(ch) != 0 {
pwm.set_duty_on(ch, MAX_DUTY);
}
} else {
pwm.set_duty_on(ch, amount);
}
}2nd strike — PWM channel duty auxiliary. For disabling channel little figure of speech is needed. For reason on this one can make own research starting at fn set_duty_on.
use core::ops::BitOr;
#[repr(u8)]
#[derive(Clone)]
enum KeyType {
Zero = 0,
Odd = 1,
Even = 2,
Prime = 4,
SafePrime = 13, // 1101, always odd
#[allow(dead_code)]
SgPrime = 20, // 10100, can be even
#[allow(dead_code)]
SgAndSafePrime = 29, // 11101, always odd
}
impl BitOr for KeyType {
type Output = KeyType;
fn bitor(self, rhs: Self) -> KeyType {
let add = self as u8 | rhs as u8;
unsafe { core::mem::transmute::<u8, KeyType>(add) }
}
}
use crate::KeyType::{Even, Odd, Prime, SafePrime, Zero};
fn key_typ(num: u16) -> u8 {
let typ = match prime_ck(num) {
PrimeCk::Zero => Zero,
PrimeCk::Two => Prime | Even,
PrimeCk::Odd => Odd,
PrimeCk::Even => Even,
PrimeCk::Prime => {
match prime_ck((num - 1) >> 1) {
PrimeCk::Prime => SafePrime,
_ => Prime | Odd
}
}
};
typ as u8
}3rd strike — key flags computation. enum KeyType holds some number property variants that can be examined on shared key. SgPrime stands for Sophie Germain's primes. Some (composed) flag values are precomputed. Do not hesitate to verify it. As #[allow(dead_code)] attribute suggests, SgPrime and SgAndSafePrime are unused and just matter of interest. Next BitOr trait implementaion for KeyType useful for flags combination. fn key_typ is responsible for examination properties of key. For this is needed information from fn prime_ck. When it has it, providing result is simple. One more interesting arm is PrimeCk::Prime. It this case fn prime_ck is used again. This time with (num -1) ÷2. If this number is prime, by definition, it is Sophie Germain prime, thus num is safe prime number. For SGP applies 2 ⋅pb +1 = pc, for SP (pb -1) ÷2 = pa, where p means prime number.
#[derive(PartialEq)]
enum PrimeCk {
Zero = 0,
Odd = 1,
Even = 2,
Prime = 4,
Two = 14,
}
fn prime_ck(num: u16) -> PrimeCk {
match num {
0 => return PrimeCk::Zero,
1 => return PrimeCk::Odd,
2 => return PrimeCk::Two,
x if x &1 != 1 => return PrimeCk::Even,
_ => {}
}
let sqrt = herons_sqrt(num);
let num = num as i32;
for i in 2..=sqrt {
if num % i == 0 {
return PrimeCk::Odd;
}
}
PrimeCk::Prime
}4th strike — prime number examination. enum PrimeCk holds possible results of prime check. One point of interest could be Two variant with 14 integer value. fn prime_ck is more interesting. Once again square root function is needed. Initial match sieve catches cases on which consequent computation would: fail or be useless. Reason behind this prime check is well known and easy understandable. Mathematically 1 < a ≤ b < num, num = a ⋅b = √num ⋅√num ⇒ a=b=√num ∨ (a < b ∧ a < √num ∧ b > √num). This means at least one factor cannot be greater than √num.
// 2962^255 ≈ 1.7955141e+885
const MAX_PLACES: usize = 886;
const MAX_U16_PLACES: usize = 5;
#[allow(non_camel_case_types)]
type decimalsU16 = ([u8; MAX_U16_PLACES], usize);
#[allow(non_camel_case_types)]
type decimalsMax = (maxPlaces, usize);
#[allow(non_camel_case_types)]
type maxPlaces = [u8; MAX_PLACES];
trait AsSlice {
fn as_slice(&self) -> &[u8];
}
trait AsSliceMut {
fn as_slice_mut(&mut self) -> &mut [u8];
}
impl AsSlice for decimalsU16 {
fn as_slice(&self) -> &[u8] {
&self.0[..self.1]
}
}
impl AsSliceMut for decimalsMax {
fn as_slice_mut(&mut self) -> &mut [u8] {
&mut self.0[..self.1]
}
}
fn to_decimals(num: u16) -> decimalsU16 {
let mut decimals = [0; MAX_U16_PLACES];
let mut ix = 0;
let mut num = num as i32;
loop {
let d = num % 10;
decimals[ix] = d as u8;
num = num / 10;
ix += 1;
if num == 0 {
break;
}
}
(decimals, ix)
}
fn from_decimals(decimals: &[u8]) -> u16 {
let mut num = 0;
let len = decimals.len();
for ix in 0..len {
let place = decimals[ix];
if place == 0 {
continue;
}
num += place as i32 * 10i32.pow(ix as u32);
}
num as u16
}5th strike — facilities for once mentioned big numbers. Most interesting is const MAX_PLACES: usize = 886;. It was stated that it is expected uncalibrated magnetomer shall not produce values that will result in magnitude greater than 2,962 µT. Reason is there sketched by comment. This value is foundation for places array size. More details later. Some useful type aliases with slice conversion functions follow. Conversion functions fn to_decimals, fn from_decimals serve for conversion of u16 to and from places array. u16 fits well because of anticipated limit 2962 implied by highest safe prime number used, 2963, and anticipation on field magnitude; any initial (generator, primes, …) or finite (modulo results) values are much lower than 216 -1.
Auxiliaries facilitate everything what is needed by hearth. But firewood comes out of somewhere else. From mathematical crisscross.
Seductive shelter full of firewood🌐
Seductive shelter full of firewood exposes its treasures to espying eyes nearby… Another type of dweller is mathematical function.
fn herons_sqrt(num: u16) -> i32 {
let num = num as i32;
if num == 1 || num == 0 {
return num;
}
let mut cur = num >> 1;
loop {
let nex = (cur + num / cur) >> 1;
if nex >= cur {
break;
}
cur = nex;
}
cur
}At last Herons's square root function. Square root produced by this function is floored but this is specific to current usages. It works fair with fractional places as well. For proof see Hero's Method on Proof Wiki.
fn pow(base: &[u8], pow: u8) -> decimalsMax {
let mut aux1 = [0; MAX_PLACES];
if pow == 0 {
aux1[0] = 1;
return (aux1, 1);
}
let base_len = base.len();
for ix in 0..base_len {
aux1[ix] = base[ix]
}
if pow == 1 {
return (aux1, base_len);
}
let mut aux2 = [0; MAX_PLACES];
let mut steps = [0; 7];
let mut wr_ix = 0;
let mut step = pow as u8;
loop {
steps[wr_ix] = step;
step >>= 1;
// `pow = 1` and `pow = 0` solved above
if step == 1 {
break;
}
wr_ix += 1;
}
let mut mcand = &mut aux1;
let mut sum = &mut aux2;
let mut mcand_len = base_len;
let mut sum_len = 0;
let mut ixes = (0..=wr_ix).rev();
loop {
let re_ix = unsafe { ixes.next().unwrap_unchecked() };
for off in 0..mcand_len {
sum_len = muladd(&mcand[0..mcand_len], mcand[off], sum, off);
}
if steps[re_ix] & 1 == 1 {
clear_swap(&mut mcand, mcand_len, &mut sum);
mcand_len = sum_len;
for off in 0..base_len {
sum_len = muladd(&mcand[0..mcand_len], base[off], sum, off);
}
}
if re_ix == 0 {
return (*sum, sum_len);
}
clear_swap(&mut mcand, mcand_len, &mut sum);
mcand_len = sum_len;
}
}fn pow power function is powerlifter. It allows to compute large results of powering needs for this DHKE implementation. Function private_generation limits power to u8 range. Thus upper limit is 255. As far as magnetic field magnitude is exptected to be reasonable imprecise, it can be anticipated that greatest base available is 2962 which is greatest possible remainder deeming greatest safe prime number 2963. While powering only generator and remainder, calculation 2962255 ≈ 1.7955141e+885 shows that places array size must be 886.
fn pow revolves 2 mathematical methods: column multiplication which first school level children are taught and exponentiation by squaring. Former is used because numbers are represented as array of numbers reprenting respective decimal places. Thus this method functions quite well. /Details will come with fn muladd./ Latter is used to speed up computations from θ(n), where n is power, to θ(log n). In fact, as measured for powers up to 255 this brings no interesting improvement. Thus it is merely matter of interest only.
fn pow simply iterates through places in multiplicand for each step generated and passes it as multiplier for multiplicand to muladd. With extension for squaring exponentiation. Aformentioned steps are quite interesting. At first glance it seems that iterating could simply rely on logarithm of base 2 for pow. But this is not case.
Let choose some number for power, like 11. Generated steps would be 11, 5, 2. ⌊log211⌋ = 3. Steps count matches, iteration starts from lowest step, (0..=wr_ix).rev();. What would happened if instead of precomputed step values were computed ones used? At first, initial value is unknown, for 13 steps are 13, 6, 3 while for 11 initial value is 2. Also each value would simple be next multiplication of 2, 3>>1 = 6, 6>>1 = 12, …. These numbers are different from steps generated and importantly are all even.
Good and valid solution would be to precompute step base using floating point numbers. For 11 this is 2.75. Steps are then computed on site using formula ⌊base ⋅2iteration⌋ where iteration is 0 based, ⌊2.75 ⋅1⌋=2, ⌊2.75 ⋅2⌋=5, ⌊2.75 ⋅4⌋=11. Powering ends when step equals power. It seems approach with steps pregeneration is only detrimental. More or less. It could be beneficial to precompute steps because floating point number computations are quite expensive. At least array of size 7 B will not stress out even such restricted device as micro:bit is. But, there is one feature that worth pointing out. When pow would not be u8 but some big number like 263-1, due FPN precision, such amount of divisions and multiplications and even conversion from integer types can be tricky. Example bellow shows that big number after conversion to has different value same as when converted from. Question arises already when div has exact value of 1.
fn main() {
let a = 2u64.pow(16) - 1;
ck(a);
let a = 2u64.pow(32) - 1;
ck(a);
let a = 2u64.pow(63) - 1;
ck(a);
}
fn ck(n_u64: u64) {
let n_f64 = n_u64 as f64;
println!("n_u64 : {}", n_u64);
println!("n_f64 : {}", n_f64);
let div = div(n_f64);
println!("div : {}", div);
let mul_f64 = mul(n_f64, div);
let mul_u64 = mul_f64 as u64;
println!("mul_f64 : {}", mul_f64);
println!("mul_u64 : {}", mul_u64);
println!("mul_u64 = n_u64 : {}", mul_u64 == n_u64);
println!("mul_f64 = n_f64 : {}", mul_f64 == n_f64);
println!();
}
fn div(n: f64) -> f64 {
let mut res = n;
loop {
let tmp = res / 2.0;
if tmp >= 1.0 {
res = tmp;
} else {
break;
}
}
res
}
fn mul(n: f64, d: f64) -> f64 {
let mut res = d;
loop {
let tmp = res * 2.0;
if tmp <= n {
res = tmp;
} else {
break;
}
}
res
}n_u64 : 65535 n_f64 : 65535 div : 1.999969482421875 mul_f64 : 65535 mul_u64 : 65535 mul_u64 = n_u64 : true mul_f64 = n_f64 : true n_u64 : 4294967295 n_f64 : 4294967295 div : 1.9999999995343387 mul_f64 : 4294967295 mul_u64 : 4294967295 mul_u64 = n_u64 : true mul_f64 = n_f64 : true n_u64 : 9223372036854775807 n_f64 : 9223372036854776000 div : 1 mul_f64 : 9223372036854776000 mul_u64 : 9223372036854775808 mul_u64 = n_u64 : false mul_f64 = n_f64 : true
Objective: If fn pow was recursive, there would be no need for steps or floating point data types. Yes, that is truth. But, then each call would allocate 2 somewhat big arrays which is not much desired in any environment, emphasizing micro:bit. This could be, of course, optimized by means of handling maximal arrays for respective power = recursion deep but this would make function logic more complex reducing memory consumption only partially. Similarly, only one array needs to be used as auxiliary for intermediate sums but then it could happen that passed-in array will not be that one with result in final round involving other round of copying. When both would be passed in, then it would be really optimal. Only some initial/post cleaning would be needed. Thus this solution is suboptimal and rather straightforward. Nonetheless, repeating allocations pose no problem.
fn muladd(mcand: &[u8], mpler: u8, sum: &mut [u8], base_off: usize) -> usize {
let mut sum_max_ix = 0;
let mut ix = 0;
let mcand_len = mcand.len();
loop {
let prod = mpler as i32 * mcand[ix] as i32;
let max_wr_ix = sumadd(prod, sum, base_off + ix);
if max_wr_ix > sum_max_ix {
sum_max_ix = max_wr_ix
};
ix += 1;
if ix == mcand_len {
break;
}
}
sum_max_ix + 1
}
fn sumadd(mut addend: i32, sum: &mut [u8], mut off: usize) -> usize {
let mut takeover = 0;
loop {
let augend = sum[off];
sum[off] = ones(augend as i32 + addend, &mut takeover);
if takeover == 0 {
break;
} else {
addend = 0;
off += 1;
}
}
off
}
fn ones(num: i32, takeover_ref: &mut i32) -> u8 {
let mut takeover_val = *takeover_ref;
let total = num + takeover_val;
takeover_val = total / 10;
*takeover_ref = takeover_val;
(total - takeover_val * 10) as u8
}It is fn muladd, fn sumadd and fn ones which does hard part of column multiplying. fn muladd computes intermediate product for each column in multiplicand. For current column product it uses fn sumadd to add it to intermidiate sum. Reason to add to sum immediately is simplicity. Otherwise result of each column product would need to be stored in some data structure before adding to sum.
3019
× 19
------
27171
3019
= 57361
= 1 + 70 + 100 + 7000 + 20000 + 0 + 90 + 100 + 0 + 30000
= 81 + 90 + 0 + 27000 + 90 + 100 + 0 + 30000 There is interesting pivot in muladd, sum_max_ix. This guards real sum length which is rather unpredictable.
3 019 × 19 = 57 361
# multiplier 1
3 019 × 9 = 27 171
# multiplier 2
3 019 × 10 = 30 190Examing fn pow, one can see how sum_len is used. And it needs to be accurate. As previous example shows, it cannot be expected that sum in next iteration is simply one place longer because of incremented offset. Having multiplier 99 at begining, it would. Since # multiplier 2 would be 90 and sum 298 881. Similarly, multiplier 91 would produce sums of len 4 (3 019) and 6 (274 729). Notional place addition is maintained by offsetting. Guarding if max_wr_ix > sum_max_ix is useful because not all sum additions are obliged to hit its top place.
Cognizant one could spot that fn muladd is suboptimal. It operates in vain for mpler = 0. Some changes are needed to support quick escape. Good exercise. Also this is subject to possible future refactoring.
fn sumadd is capable of correctly adding to intermediate sum. It adds to place specified value specified. If needed it iterates as long as needed to add carried-on values to next places. As example bellow gestures towards, sumadd uses column addition.
| #1 #2 #3 result
------------------------------------------
sum | 109700 109600 100600 110600
place | ^ ^ ^
addend | 9 1 1
Column multiplication and column addition are slightly modified as presented. Multiplication sum is computed immediately not from rows and addition can start with tens. Nonetheless methods are clear.
sumadd cannot work without fn ones. fn ones has simple responsibility. It extracts ones (place) from arbitrary (i32) number after summing it with carried-on value from previous iteration and returns both: ones and left over value which basically is also ones. Terminology became slighty chaotic but from ones point of view input number is "set free from" its ones. It does not matter whether actual num pertains to another place than ones.
Function chain muladd, sumadd, ones can be slightly opaque at first glance. Let say prod was 81 = 9 ⋅9, augend was 9 and takeover was 0. Then total would be 90, ones would return 0 and takeover_ref would be 9. From properties: maximal product = 81, maximal augend = 9, maximal initial total = 90 implication that takeover is always ones place can be drawed out (since maximal next total = 18 = 9 +9, maximal other total = 10 = 9 +1).
There is one more function on which fn pow is dependent, fn clear_swap.
fn clear_swap<'a>(mcand: &mut &'a mut maxPlaces, mcand_len: usize, sum: *mut &'a mut maxPlaces) {
for ix in 0..mcand_len {
mcand[ix] = 0;
}
let swap: *mut maxPlaces = *mcand;
unsafe {
*mcand = *sum;
*sum = swap.as_mut().unwrap_unchecked();
}
}fn clear_swap is responsible for placing intermediate sum "into" multiplicand and clearing actual multiplicand in order to allow it to serve as intermediate sum in next loop iteration.
fn rem(dividend: &mut [u8], divisor: &[u8]) -> u16 {
let mut wdsor = [0; MAX_PLACES];
let mut end_len = dividend.len();
let sor_len = divisor.len();
let sor_hg_ix = sor_len - 1;
while end_len > sor_len {
let mut wr_ix = end_len - 1;
let mut l_ix = wr_ix;
let mut r_ix = sor_hg_ix;
loop {
let end_num = dividend[l_ix];
let sor_num = divisor[r_ix];
if end_num < sor_num {
wr_ix -= 1;
break;
} else if end_num > sor_num {
break;
}
if r_ix == 0 {
break;
}
l_ix -= 1;
r_ix -= 1;
}
let wdsor_len = wr_ix + 1;
let mut sor_ix = sor_hg_ix;
loop {
wdsor[wr_ix] = divisor[sor_ix];
if sor_ix == 0 {
break;
}
sor_ix -= 1;
wr_ix -= 1;
}
end_len = rem_cross(dividend, &wdsor, end_len, wdsor_len);
}
if end_len == sor_len {
end_len = rem_cross(dividend, divisor, end_len, sor_len);
}
from_decimals(÷nd[..end_len])
}Another round of attractive mathematics. fn rem serves for remainder computation. Since remainder is in fact computed in fn rem_cross by column substraction, it would take entire eternity to compute it. rem avoids this by repeatedly extending divisor to highest possible 10 multiplication and substracting widen divisor from dividend. As long as original divisor can be widen.
35831808 = 127
35831808 mod 17 = 7
#1 35831808 - 2·17000000 = 1831808
#2 1831808 - 1·1700000 = 131808
#3 131808 - 7·17000 = 12808
#4 12808 - 7·1700 = 908
#5 908 - 5·170 = 58
#6 58 - 3·17 = 7
Widening occurs in rem while (repeated) substraction in rem_cross. For illustration 35831808 ÷ 17 ≅ 2 107 753 (= substraction count). Much compared to demands provided by divisor widening. Little compared to requirement would involved by actual implementation calculations. E.g. 123412 ÷ 1235 ≅ 10095200730507359721104453683166373. While maximum anticipated value is 2962255. Divisor, 2963, would end up with terrible computation times same as every other as long as dividend is considerably large.
fn rem_cross(end: &mut [u8], sor: &[u8], end_len: usize, sor_len: usize) -> usize {
let mut takeover;
let mut ix;
loop {
takeover = 0;
ix = 0;
while ix < end_len {
let sor_num = if ix < sor_len {
sor[ix]
} else if takeover == 0 {
break;
} else {
0
} as i32;
let mut end_num = end[ix] as i32;
let total = sor_num + takeover;
takeover = if end_num < total {
end_num += 10;
1
} else {
0
};
end[ix] = (end_num - total) as u8;
ix += 1;
}
if takeover == 1 {
ix = 0;
takeover = 0;
let mut not_len = 0;
while ix < sor_len && ix < end_len {
let correction = end[ix] as i32 + sor[ix] as i32;
let one = ones(correction, &mut takeover);
end[ix] = one;
if one == 0 {
not_len += 1;
} else {
not_len = 0;
}
ix += 1;
}
return if not_len == ix { 1 } else { ix - not_len };
}
}
}Beside aforementioned column substraction, fn rem_cross is interesting by logic involved in resolving substracting end and correction of actual state. It is unpredictable how many substracting will there be thus end dictates fact that borrow was not satisfied which means number was "substracted bellow zero", if takeover == 1. Under this state result is oversubstracted and must be corrected by (column) addition back to remainder.
Assembled altogether🌐
Compared to requirements, result is moderately unsatisfactory. Nonetheless, here it is.
Whole project at Mismash (gh repo).
[package] name = "mishmash" version = "0.0.1-alpha" authors = [ "software9119.technology" ] edition = "2021" license = "MIT" [dependencies] lsm303agr = "0.3.0" microbit-v2 = "0.13.0" cortex-m = "0.7.3" cortex-m-rt = "0.7.0" panic-halt = "0.2.0"